At the beginning of this year I committed to publishing regularly on this substack. I was wrong. Life happened, and I had to abandon that commitment. I have instead focused on finishing my book, The Return of the Great Mother. It won’t be done anytime soon, but barring a rogue bus or act of God, it will be finished.
What follows is a brief excerpt from the book’s introduction, which outlines its structure, followed by the current draft of Chapter 1. I won’t publish every chapter here, but this one stands alone—an essay on the practical implications of complexity science and dynamical systems theory. Think of it as a teaser, a taste of what’s to come.
If you make it to the end, you’ll understand what is meant by “The Strange Attractor at the Heart of Myth”.
Below is the excerpt from the introduction.
How This Book is Structured
This is not a book for passive consumption.
It is not a self-help manual. It is not a pop-philosophy digest. It is not designed to entertain you, flatter you, or reassure you.
This book is a descent and a return. It is a map of the psyche, of the world, of the myth we are living through and the one we must breathe new life into. It is meant to show you that the deep structure of the psyche, the world, and of that myth are the same.
It unfolds in four parts, each distinct in tone and purpose:
Part One: Order and Chaos
This is the foundation—dry, technical, rigorous. It is the least “literary” portion of the work, but perhaps the most essential. Here we lay down the scientific bedrock:
Dynamical systems theory
Self-organized criticality
Evolutionary psychology
Behavioral genetics
Cultural evolution
The diametric model of autism and psychosis
Hemispheric differences
Relevance realization
Scientific theories of consciousness
This is not a story. It is a toolkit.
These chapters form the foundation of the book—and that foundation is not speculation, but mainstream science. What follows is a survey of established scientific literatures: dynamical systems theory, evolutionary psychology, and more. Each is necessary.
If you skip this part, you will not be prepared for what follows.
Part Two: The Rise of Urizen
This is the genealogy of nihilism.
Urizen is a figure drawn from the poetry of William Blake—a god of law, division, and abstraction. He is Yahweh’s shadow, the architect of reason without soul. He is Blake’s poetic description of our modern malaise. In this section, we trace the evolutionary, cultural, and historical forces that gave birth to the modern self—and to its crisis.
We look at how God died—not as a single event, but as the culmination of a process that stretches back for millennia. We examine how the modern mind was built—and why it can no longer bear its own weight.
This part sets up the problem we must solve.
Part Three: The Return of the Great Mother
Here, the story turns.
What was shattered must be reassembled—but not in the old forms. The Great Mother is not a person. She is the symbolic return of the primordial chaos, the mythic womb, the archetype that comes rushing back when the Father-God dies.
This section is neither a scientific treatise nor a historical record. It is a mythopoetic synthesis, an attempt to show that what lies at the border between order and chaos is not a metaphor—it is a percept. It is raw power that must be felt and seen rather than theorized.
The sacred process that emerges at this border does not require belief.
Part Four: The Adversary
There are those among us who hunger for chaos—sometimes openly, but most often cloaked in the garb of compassion, grievance, or righteous fury. And there are others who cannot abide the strange, the deviant, the untamed—those who seek to crush all variance in the name of control and security.
Both are adversaries to the delicate process that emerges at the border between order and chaos.
In Part Four, we will trace the origins of these two psychological archetypes—the ones Jordan Peterson named decadent and fascist. One seeks dissolution; the other, calcification. One would burn the world in the name of liberation, the other would freeze it in the name of obedience.
They are not abstractions, nor are they merely trolls behind computer screens. When either type seized the levers of power in the 20th century, the cost was catastrophic. Tens of millions died.
We will examine their psychological and mythological roots, their evolutionary origins, and—most importantly—how to recognize them when they come cloaked in virtue.
And now, here is Chapter 1 of Part One.
It begins, as it must, with motion.
Enjoy.
Chapter 1: The Dynamics of Becoming
Out of life’s school of war: What does not destroy me, makes me stronger.
- Nietzsche
Why do some habits seem impossible to break, while others collapse overnight? Why do societies and economies lurch from stability to crisis with no clear warning, or people undergo sudden transformations after years of stagnation? These aren’t just psychological or sociological puzzles—they’re signatures of a deeper structure: dynamical systems. This chapter offers a new vocabulary for understanding such systems—entities that complexify over time, shaped by feedback, history, and context. We will explore how to visualize them using phase space, how they stabilize into attractors, how perturbations can trigger profound phase transitions, and why, in complex living systems, true resilience emerges not from stability, but from the capacity to transform.
We will see how living systems endure by changing, not by staying the same. In scientific terms, they are dissipative structures—systems that sustain order through motion. This insight, long intuited by philosophers and mystics1, has become a cornerstone of complexity science and dynamical systems theory.
We draw here especially on the work of philosopher of science Alicia Juarrero, who argues that traditional models of causation and control are not just outdated—they’re dangerous. These models equate order with stability. That’s a fine attitude for teacups; disastrous for people and cultures. To understand the risk, we must first explore the alternative: the temporally sensitive, constraint-based model of causation developed in Juarrero’s 2002 book Dynamics in Action.
In the classical Newtonian picture, causes work like billiard-balls: one thing bumps another, producing a chain of discrete impacts. But this model fails spectacularly when we try to explain complex behavior in organisms, cultures, and other dynamical systems. These systems are not merely pushed along from the outside; they are self-directed, goal-oriented, and intentional. Understanding the behavior of complex systems requires a different understanding of causation.
There is, in fact, a well-established philosophical framework that predates modern science by two millennia—one that is far better suited for making sense of complex, living systems. Around 2,400 years ago, Aristotle introduced the four types of causation:
1. Efficient Cause – That which strikes, pushes, initiates. The arrow flies because the bowstring snaps; the man speaks because neurons fire; the temple collapses because the earthquake shakes the ground. This is the only cause that modern scientists recognize—because it can be measured, graphed, and replicated. It is force, movement, the shove of one thing against another. But it is not enough. It is the surface of causality—a fragment of the picture, mistaken for the whole.
2. Material Cause – That from which a thing is made. The bronze in the statue, the blood in the body, the stone in the monument. This is the substance, the clay. Yet clay alone does not explain the sculpture—it must be formed, shaped, destined.
3. Formal Cause – The blueprint, the organization, the configuration that makes a thing what it is. A car disassembled is just a pile of parts; it becomes a vehicle only when those parts are arranged in a specific way. Identity lies not in the matter, but in the pattern. The same steel can form a scalpel or a sword—form decides the role. In today's terms: systems theory, code, design. Form is what turns components into function—what enables parts to act as a whole.
4. Final Cause – The goal, the purpose, the direction of a process. A seed becomes a tree not because it is pushed from behind, but because it is organized toward a future form. Final cause does not imply conscious intention—it simply means that some systems are structured to move toward ends. In biology, this is known as teleonomy: goal-directed behavior shaped by evolution. Organisms act in ways that preserve themselves, seek nourishment, reproduce. Their behavior is not purely reactive—it is oriented. Deny this and you may succeed in describing their anatomy, but you will fail to understand their development and behavior.
For simple, linear systems—like a pendulum or a two-body orbit (e.g., the interactions between Earth and its moon)—efficient causation works beautifully. These are systems where the future unfolds from the past like a spool unwinding, where force and mass and motion can be cleanly tracked and mathematically predicted. In such domains, efficient cause is not just adequate—it is elegant. The Newtonian framework is prized not only for predictive power but for its mathematical beauty, unifying terrestrial and celestial motion under the same principles. But elegance becomes a noose when mistaken for universality.
Try to explain the behavior of a living system—say, a person falling in love or a bird building its nest—with efficient cause alone, and you quickly descend into absurdity. Modern philosophers, especially of the analytic breed, have spent over a century writhing under this problem, trying to explain intention without ends, structure without form, agency without aim. The deeper tragedy, as Juarrero and others have pointed out, is that modern philosophy chose this blindness. It exiled teleology—not because it was refuted, but because it was simply scoffed at. Final and formal causes were cast out as superstitious metaphysical relics, too ethereal for the cold calculus of the Enlightenment. Yet here they return, not as superstition but as necessity. Living systems are goal-directed. They act toward futures that do not yet exist, and those imagined futures constrain and shape present behavior. Biologists call it teleonomy, but the name doesn’t matter. The reality does. This is final causation.
This is where the concept of constraint becomes crucial. A constraint is not a force—it doesn’t push—but it changes what is possible. It modulates behavior by narrowing the space of viable options. In physical terms, it defines the phase space—the set of all potential states a system can occupy—and then sculpts it, fencing off some regions, deepening others, forming basins, barriers, and gradients. The result is that some behaviors become more likely, others less so, and some altogether impossible. In this way, constraints shape causality not by producing motion, but by guiding it.
Consider the game of chess. A knight does not move randomly across the board, nor is its motion dictated solely by any mechanical force. Its behavior is constrained by the rules of the game, which define how and where it can move. The rules don’t push the knight, but they determine the structure of what movement is valid. The cause of the knight’s movement, then, is a conjunction of its position, the player’s intention, the mechanical force of the player’s hand and arm, and the abstract constraints that define the system of chess itself.
What Is a Dynamical System?
Before we can fully understand why it was necessary to resuscitate the notions of formal and final cause, we must first be clear about what is meant by a dynamical system. A dynamical system is any system whose state evolves over time according to a set of rules. But unlike the idealized, closed systems of classical mechanics, dynamical systems are typically open, historical, and context-sensitive. They are time-dependent—what happens now depends not only on present inputs, but on the system’s past. They are path-dependent—two systems with identical components can behave differently depending on the sequence of states they've passed through. And they are nonlinear—a small change in initial conditions can produce disproportionate, often unpredictable effects. This nonlinearity is most famously known as the butterfly effect.
Dynamical systems often involve feedback loops—recursive interactions between components that can amplify or dampen behavior. Because of these features, dynamical systems exhibit emergence: novel, coherent patterns arise that are not predictable from the behavior of individual parts alone. This makes them radically unlike the mechanistic systems envisioned by early modern science. And it is precisely these properties—recursion, emergence, sensitivity to history—that make dynamical systems theory indispensable for understanding cognition, behavior, society, and life in general.
Consider this relatively simple example of a dynamical system: a pot of water on the stove. As heat is applied, nothing seems to happen for a while—until, suddenly, bubbles form. This qualitative shift is called a phase transition or phase change. Any attempt to explain this transition solely in terms of individual molecular collisions—efficient causes in the classical sense—proves to be woefully inadequate. Statistical mechanics succeeds precisely by abandoning this atomistic approach and modeling the system in terms of emergent behavior governed by statistical regularities and shaped by macroscopic constraints (e.g., energy, number of particles, volume). The pattern of boiling is emergent—shaped by macroscopic constraints like temperature, pressure, the container, and feedback among the approximately 1 x 10^26 molecules. The past matters; the path to this state matters. The transition is nonlinear, abrupt. No single molecule ‘causes’ boiling. The system as a whole transforms.
If efficient causation is insufficient to explain the behavior of boiling water, it is infinitely more inadequate in explaining the behavior of living creatures. Unlike water molecules, many organisms interpret, anticipate, and constrain their own responses based on memory, context, and imagined futures. A person avoids a dark alley not because they are physically repelled, but because they remember a story, recognize a pattern, feel a threat, and make a decision. Efficient causation might explain the contraction of muscle fibers, but it cannot account for why the step was taken, what it meant, or how it was selected among countless alternatives. Living systems act not only under external pressure, but within internally structured landscapes of possibility—landscapes sculpted by evolution, habit, emotion, desire. These are not external forces—they are constraints and attractors, shaping behavior from within. And it is here, in the realm of intentionality and emergence, that formal and final causes reassert their relevance—not as metaphysical luxuries, but as indispensable tools for making sense of life.
Maps of Motion: Describing a Dynamical System
To understand how dynamical systems behave, we must learn how to represent them. Unlike simple mechanical systems, which can often be described with a few equations or variables, complex dynamical systems require a more holistic approach. The primary tool used to model their behavior is something called phase space—a conceptual landscape in which each possible state of the system corresponds to a unique point. As the system changes over time, it traces a path through this space, called a trajectory. Phase space does not represent physical space, but the totality of a system’s conditions at a given moment: position and momentum, mood and motivation, temperature and pressure—whatever variables are relevant to the system in question. Each variable adds a dimension, making most visual models dramatic oversimplifications of a system's true complexity. Unfortunately, we have not yet evolved the capacity to visualize more than a few dimensions, not to mention the hundreds or thousands of dimensions involved in a typical complex system. While necessarily a simplification, phase space allows us to visualize and analyze the dynamics of these systems. We are no longer asking merely what a system is, but how it moves—what paths it traces, what futures it leans toward.
Below is a simple representation of phase space.
Imagine the red ball as the current state of a system—say, a person’s mood, a cultural practice, or even a political regime. The curved blue line represents the contours of the phase space: the deeper the valley, the more stable that state is. These valleys are called attractors—regions toward which the system naturally drifts and remains over time. In this image, Attractor A is a shallow basin; the system is currently “stuck” there. Attractor B, by contrast, is deeper—more stable—but also harder to reach. Moving from A to B would require a perturbation strong enough to push the system over the hill that separates them. This is one way to understand path dependence and systemic inertia: the system doesn’t simply go where it “should,” it goes where the landscape allows—and only dramatic interventions can shift it from one basin to another.
While real-world systems almost always occupy many more dimensions than the two shown in the image above, this simplified landscape still helps us to grasp the core idea. Consider a social media platform like X, Facebook, or Substack. We can model the platform as a dynamical system, with different attractor states corresponding to different patterns of user behavior. In this model, Attractor A represents a state dominated by outrage cycles and algorithmic echo chambers. Attractor B, by contrast, represents a state of thoughtful discourse—calmer, slower, more deliberative.
If the platform is currently resting deep in Attractor A, small design tweaks—minor policy changes or tweaks to the feed—are unlikely to induce a phase transition. The system has too much inertia. Only a significant disruption—an overhaul of algorithms, a mass exodus of users, or a radical policy change—could provide enough perturbation to push the platform out of one basin and into another. And even then, there’s no guarantee: the system could just as easily fall back into its old attractor, unless new constraints reinforce the new state.
The Varieties of Attractors
So far, we’ve spoken of attractors as if they were simple wells—places a system settles into and stays. But this only describes one particular kind of attractor. In fact, the shape of an attractor can tell us a great deal about how a system behaves over time. Some attractors, like the ones represented in the image above, pull a system toward a fixed point; others draw it into rhythmic cycles; still others give rise to unpredictable, turbulent motion that never repeats and yet never escapes. These differences are not decorative—they define the stability, rhythm, and volatility of the system’s behavior. To understand these patterns, we need to examine the major types of attractors found in phase space: point, periodic, and strange.
A point attractor, represented by the diagram above, is the simplest kind of dynamical end-state. It draws the system toward a single, stable configuration—a resting point. Once the system arrives at this state, it stays there unless perturbed. Think of a marble dropped into a smooth bowl: no matter where it starts, it rolls down to the bottom and settles. In biological or psychological terms, a point attractor might represent homeostasis—our body returning to a set temperature of 98.5 degrees Fahrenheit—or a fixed belief that stubbornly remains in the face of conflicting information. In some cases, a point attractor can be healthy stability; in others, it can represent stasis and stagnation. The key is that motion ceases. From the perspective of phase space, all trajectories in the surrounding area spiral or fall inward toward a single point. The story of the system, once it reaches the attractor, is over—unless something intervenes.
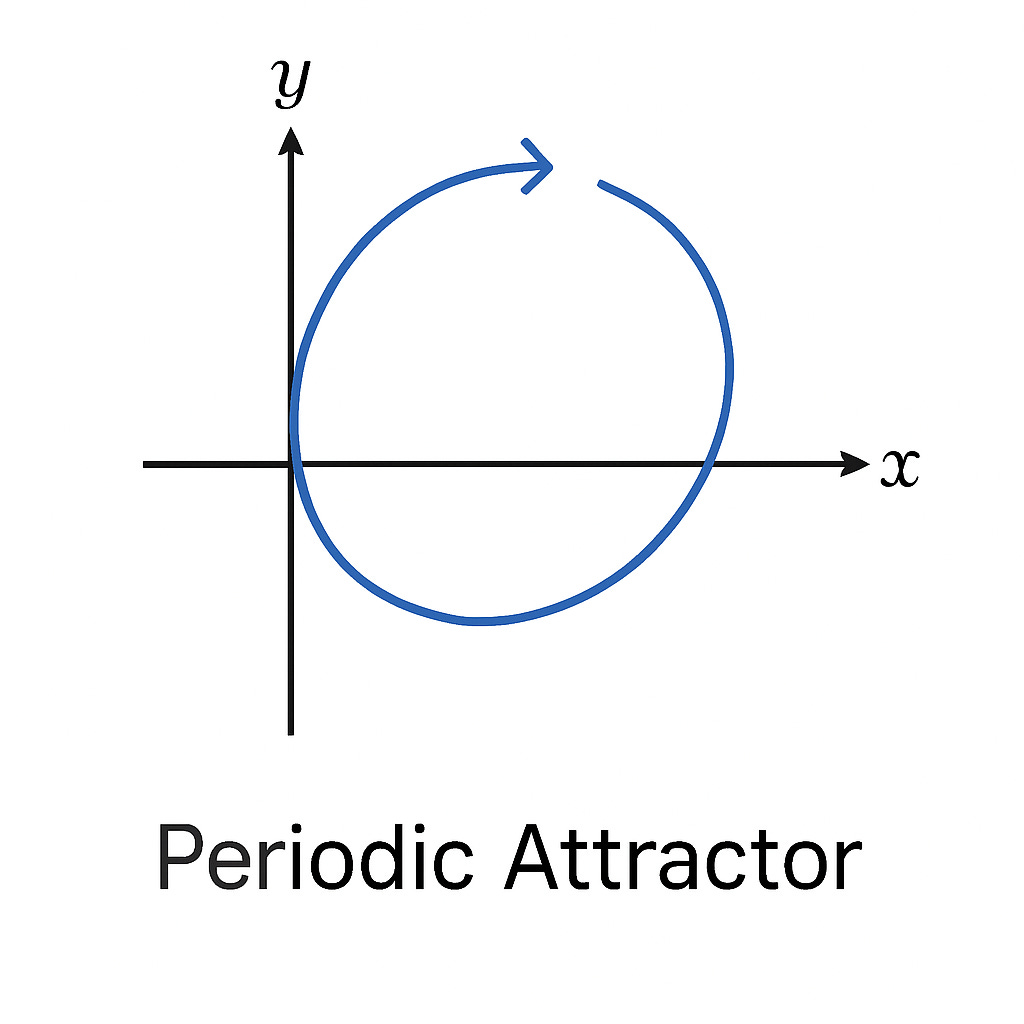
A periodic attractor draws a system into a stable cycle—an endlessly repeating loop of behavior. Unlike a point attractor, where the system converges to a single stable point, a periodic attractor represents oscillatory or cyclic behavior: not stillness, but predictability. The simplest example is a swinging pendulum, moving back and forth in a regular arc. Biological systems are full of periodic attractors: circadian rhythms, the heartbeat, menstrual cycles, predator-prey oscillations. In the brain, certain emotional or cognitive states can also loop—worry feeding on itself, or addiction cycling between craving and reward. In phase space, these would be represented by closed loops: once entered, the system moves predictably through the same sequence of states. Periodic attractors give rise to order, but it is a repetitive order—self-renewing, yet potentially rigid. In excess, they become rut and mindless ritual. But in balance, they form the vital rhythms of life. Below is an image representing a simple periodic attractor.
There is technically another type of attractor — something in between a periodic and strange attractor — called a torus attractor that will not play any role in this book and so won’t be discussed at length. To put it simply, torus attractors are quasi-periodic. They never quite repeat, but still follow a predictable, structured path. While strange attractors (discussed below) are highly sensitive to initial conditions and therefore unpredictable, torus attractors are not. They are far more orderly.
Strange attractors are the most important kind of attractor we will discuss in this book. They describe a system that is neither chaotic in the colloquial sense (their behavior isn’t random) nor orderly in the classical sense (their behavior isn’t predictable). The strange attractor is, instead, a region in phase space where the system’s behavior remains bounded, but never settles or repeats. Juarrero emphasizes that strange attractors are the signature of nonlinear, complex systems that are simultaneously constrained and free—systems like brains, ecosystems, cultures, and individual human behavior. They exhibit structure without predictability, coherence without repetition. In such systems, even slight variations in initial conditions can yield profoundly different trajectories over time, yet those trajectories remain confined to a particular region. This is not randomness, but determinate unpredictability: a system that unfolds according to internal rules, yet resists reduction to formulas. In the human world, strange attractors describe those patterned behaviors that define personality, mood, and habit—not mechanical repetition, but context-sensitive recurrence shaped by history, circumstance, and constraint.
Below is an image of one of the most famous strange attractors, known as the Lorenz attractor.
As Juarrero makes clear, strange attractors dwell at the border between order and chaos. Push too far into chaos, and the system dissolves: no attractor, no pattern, just noise—behavior that is unbounded and truly random. Push too far into order, and novelty vanishes: the system locks into point or periodic attractors, cycling predictably, frozen in repetition. A strange attractor holds the tension. It exhibits boundedness (order)—the system remains confined to a finite region of phase space—but without ever repeating itself. It exhibits sensitivity (chaos)—small perturbations can redirect its trajectory dramatically, but not arbitrarily. It is stable, but never still. Structured, but never static.
Attractors, as conceived within nonlinear dynamical systems, can be understood as modern counterparts to Aristotle’s formal and final causes, reinterpreted through the lens of complexity theory. A strange attractor defines a structured yet flexible basin of behavioral possibilities—a topological form that constrains trajectories without dictating them rigidly. This “form” is not statically imposed from without, but dynamically emergent from the system’s own internal interactions, echoing Aristotle’s formal cause, which gives a thing its defining essence. Yet attractors also exhibit purposiveness: they guide a system toward stable patterns of behavior across time, resisting disorder, much like Aristotle’s final cause, the telos or end toward which a process unfolds. The oak tree is the attractor that guides the development of the acorn — its final cause. As Juarrero emphasizes, such attractors do not merely describe passive regularities but embody active constraints—context-sensitive, history-laden, and enabling—that channel the system's development while allowing for novelty and individuation. In this way, attractors offer a scientifically grounded means of reintroducing form and purpose into our causal vocabulary—not by reviving Aristotelian metaphysics wholesale, but by revealing how teleological, purpose-driven organization can emerge from within the dynamics of the system itself.
I will get ahead of myself slightly here, but it must be said: the central process at the heart of this book—the process that makes life adaptive, complex, and capable of transformation—is itself best understood as a strange attractor. This process emerges at the border between order and chaos in complex systems. This insight — that optimal behavior emerges at the border between order and chaos — will reappear many times throughout this book. For now, it is enough to note that complex, optimal behavior lives in this space: neither fully predictable, nor purely random, but dynamically suspended between the two. That is where true novelty emerges. That is where complexification occurs.
Order and Chaos in Dynamical Systems
How do we model a system that is too chaotic—or too rigid—using phase space?
Imagine a landscape so flat that every point is equally accessible. The system, unconstrained, drifts without pattern or purpose. In phase space, this corresponds to total randomness: no basins, no attractors, no direction—just undifferentiated noise. This is a theoretical limit, of course; real systems never behave in a way that is completely random. But it marks one extreme of the spectrum.
At the other extreme, imagine a phase space shaped by steep mountains (also called repellers) and deep, narrow basins. Once the system falls into one of these attractors, it is nearly impossible to escape. It becomes stuck—repeating itself, unresponsive to context. This is excessive order: too little flexibility, too much constraint.
Interestingly, certain mental conditions have been modeled in terms of these phase space dynamics. Schizophrenia and acute psychosis have been associated with a phase space that is too flat: the mind leaps between thoughts with no stable ground, generating chaotic associations, hallucinations, and disorganized speech. Mental chaos. By contrast, obsessive-compulsive disorder has been modeled with a phase space that is too rigid—attractors that are too deep, repellers that are too steep. The system gets caught in repetitive patterns: rituals, fixations, narrow routines. Both extremes illustrate the same principle: mental health depends on the structure of the attractor landscape. Too flat, and we lose control. Too steep, and we become rigid, repetitive, unable to adapt. These principles apply not only to mental health, but to the health of all complex dynamical systems.
Fail-Safe vs. Safe-Fail: A Lesson in Fragility, Resilience, and Metastability
The concepts explored above are not mere abstractions. They contain important practical lessons for how we live our lives and structure our societies. In classical engineering, the gold standard was the fail-safe system—one designed to eliminate all risk of failure through layers of control, precision, and redundancy. But in the nonlinear world of complex living systems, the fail-safe standard is a trap. When disruption is inevitable, systems built to resist it at all costs grow brittle. They collapse under pressure. Resilience, by contrast, demands a different strategy: not fail-safe, but safe-fail.
As Alicia Juarrero argues, resilient systems must absorb perturbation rather than avoid it. In fact, resilient systems often seek out perturbations for exactly this purpose. Resilient people take risks and constantly expose themselves to novelty and discomfort. The resilient system must allow for small, recoverable failures—because failure is not just unavoidable, but necessary for adaptation. This principle, drawn from complexity science, holds implications beyond engineering. It applies to institutions, ethical systems, and to the development of character itself.
A teacup demands stability. Perturbations do not make it more resilient; they simply increase the risk that it will shatter. We are not teacups. Like other complex adaptive systems, we require perturbations to grow and thrive. I’ve watched too many elderly people deteriorate—mentally and physically—within months of retirement. With no challenges to face and little reason to leave the house, they stagnate, retreating into passive consumption and brittle routine. The same is true of children who are not exposed to adversity. As Jonathan Haidt and Greg Lukianoff document in The Coddling of the American Mind, children protected from difficulty do not flourish. They become fragile—easily overwhelmed, emotionally brittle, incapable of withstanding the smallest shock. When they enter adulthood, they demand stability: safe spaces, trigger warnings, and other such protections from mental or emotional perturbation. Haidt is not the only professor to comment on the “stunning fragility” of his sheltered college students.
Ancient wisdom and modern science converge on this point: what does not kill us makes us stronger. But let us not be fools. Getting hit by a bus doesn’t build character, even if we survive. Perturbations must be proportionate—challenges tuned to the system’s capacity to learn, adapt, and grow. What we need is intelligent exposure to entropy. Fragility cowers behind walls. Resilience dances with danger and grows.
This distinction—between fail-safe rigidity and safe-fail adaptability—can be directly mapped onto the logic of dynamical systems. Recall that in phase space, systems are drawn toward attractors: patterns of behavior that the system tends to return to and remain within. But not all attractors are equal. A deep, narrow attractor may offer short-term stability, but at the cost of flexibility; once the system enters it, escape becomes nearly impossible without extreme disruption. This is the logic of fail-safe design: contain chaos, prevent deviation, resist change. But resilience demands a different topography—shallower attractors, looser couplings, flexible constraints. In a safe-fail system, the landscape is rugged but traversable: the system can be perturbed, shifted, even knocked temporarily off course without collapsing entirely. In this view, failure is not a threat to order—it is necessary for its ultimate maintenance. Learning, adaptation, even creativity arise from these excursions. In complex systems, survival depends less on resisting change than on absorbing it, integrating it, and reorganizing in response.
Let’s return to the simple phase space we explored earlier so that we may better understand why perturbation is necessary for growth.
Attractor A represents the system’s current state. Attractor B, for our purposes, is a more adaptive or resilient configuration. But as the image suggests, the system is stuck—trapped in the basin of Attractor A. How can it escape? The answer is perturbation. Without a disturbance strong enough to jolt the system out of its current valley, it will remain locked in place. Only through disruption—a temporary flattening or shaking of the attractor landscape—can the system explore alternative trajectories. Safe-fail design encourages this exploration by making perturbation survivable, even desirable. By contrast, a fail-safe system rejects all disturbance and, in doing so, rejects the possibility of transformation. If the system avoids disruption entirely, it cannot discover more resilient or desirable configurations. Resilience, then, does not mean resistance to change—it means openness to transformation without total collapse.
This ideal—safe-fail rather than fail-safe—leads to a deeper conclusion: that the goal of a complex dynamical system is not stability in the classical sense, but metastability. A metastable system does not cling to a single configuration; it endures through transformation, not in spite of it. Rather than settling permanently into a rigid attractor, the system remains poised near the edge—flexible, responsive, capable of reorganizing in the face of change. As you may have guessed, metastability emerges at the border between order and chaos. The attractor landscape must not be too steep, nor too flat. Too much order is rigidity. Too much chaos, incoherence. This metastability is the form of resilience that living systems require: not a fortress against entropy, but a structured dance with chaos. It is this capacity that institutions, ecologies, and selves must cultivate if they are to survive and thrive in a rapidly changing world.
Narrative and Myth: Explaining the Unexplainable
There is one more lesson we must draw from our study of dynamical systems. In contrast to the timeless determinism of Newtonian mechanics, the behavior of complex systems is highly dependent on time and context. Their actions depend on where they've been and what's happening around them, factors that scientific laws and equations can never fully capture. The tools that explain the falling of apples and the orbits of planets—tools built for closed systems governed by linear causality—fail in the face of nonlinear, open-ended transformation. When systems undergo radical change—when they leap, rupture, reorganize—the capacity for prediction breaks down. Something else is needed.
That “something else” is narrative. When a system undergoes a phase transition—when it shatters one form and coheres into another—there is no continuous curve to trace. There is no equation or algorithm that can map the transition from state A to state B. What we need instead is a retrospective reconstruction: a way to make sense of how the system got here, what perturbation pushed it past the edge, and why it reorganized in just this way and not another. This is not mechanistic explanation. It is genealogical storytelling. It is through this lens—narrative, not calculation—that we begin to understand phase transitions in evolution, in societies, and in selves.
Consider an alcoholic man who undergoes a sudden religious conversion after fifteen years of drifting in and out of shelters, lost to addiction. One day, an otherwise ordinary phone call from his adult daughter jolts something awake. In her voice, he hears an echo of his ex-wife. A fleeting thought crosses his mind—If I don’t change, she’ll leave me too. A wave of recognition crashes over him. He smashes his last bottle of whiskey and vows never to drink again. That night, his mind is flooded with images of Jesus Christ, whom he comes to embrace as Lord and savior. He gets better. He finds work, reconnects with family, and becomes a stable presence in his grandchildren’s lives.
Stories like this are not uncommon. And they cannot be captured by scientific laws alone. No equation could have predicted that this particular phone call, at this particular moment, would catalyze such a profound transformation. The man’s history, emotional state, beliefs, regrets—all of it mattered. The past shaped the attractor he was stuck in; the call served as the perturbation that knocked him into a new basin. It is only through narrative—retrospective, interpretive, particular—that we can understand what happened.
This is true of all phase transitions in complex systems. They resist explanation by static laws or universal equations. Every rupture is particular—tied to a system’s history, its internal tensions, its precise moment of instability. But this raises a deeper question: if the specifics of transformation must be told as stories, can we still grasp the structure of transformation in general? Is there a general pattern, shape, or logic that underlies how complex systems reorganize into novel configurations?
This is where myth becomes indispensable. In his 1999 book Maps of Meaning, Jordan Peterson argues that ancient myths are not arbitrary fictions, but symbolic maps of transformation. They encode, in narrative form, how human beings and societies respond to disruption, descend into chaos, and emerge—if they are lucky—renewed. Peterson does not speak in the language of dynamical systems. He does not mention attractors, phase space, or perturbation. Yet his “meta-myth”—the recurring arc that underlies hero myths across cultures—is structurally identical to the pattern we’ve seen in complex systems: a stable state is disrupted, a descent into uncertainty follows, and a new, reconfigured order emerges.
This diagram from Maps of Meaning captures the essential rhythm of phase transitions in complex systems. The system begins in a relatively stable state—what dynamical systems theory would call an attractor. But then something breaks the spell: an anomaly, a contradiction, a stressor the current system cannot absorb. This perturbation disrupts the stability of the system, temporarily flattening the attractor landscape and plunging the system into a period of disorder—Peterson calls this a descent into “chaos”, the encounter with the unknown. If the system is resilient, this turbulence gives way not to collapse, but to reorganization. A new attractor forms—more integrated, more complex, better attuned to the world that produced the anomaly. The system does not return to its previous state. It becomes stronger through rupture.
Not all myths follow this transformative arc. Some are tragedies, in which the system—be it a hero, a culture, or a kingdom—collapses and is never restored. Others, like the myth of Sisyphus endlessly rolling his boulder uphill, depict cycles of futility rather than genuine transformation. The pattern we’re concerned with here—the descent into chaos, followed by reconstitution at a higher level—is characteristic of the type of myth that Joseph Campbell called the hero’s journey. This archetype, explored in depth in The Hero with a Thousand Faces, describes the structure of myths in which confrontation with the unknown leads not to ruin, but to renewal. Though we’ll explore the meta-mythology’s origin and structure more fully in Part 3, let us look now at a concrete example to bring the pattern into focus.
The Lion King as Metamyth
Rather than draw from ancient myth, let’s turn to a modern one: The Lion King. It follows the hero’s journey with remarkable fidelity. After a childhood trauma, Simba retreats into a behavioral attractor defined by denial, hedonism, and emotional avoidance—“Hakuna Matata.” The system is stable, but stagnant.
Then, a perturbation. Nala, the childhood friend—and anima figure—appears. Her judgment pierces the illusion, and Simba is shaken out of his equilibrium. He flees into the wilderness—his chaos phase.
As is common in these stories, the hero does not face transformation alone. A wise guide appears—Rafiki, the wise old man and shaman master. Rafiki’s role is not to impose direction, but to catalyze insight. In a brief but profound exchange, Rafiki delivers the moral logic of metastability:
Simba: Looks like the winds are changing.
Rafiki: Ah, change is good.
Simba: Yeah, but it’s not easy. I know what I have to do, but going back means I’ll have to face my past. I’ve been running from it for so long.
Rafiki: (Whacks Simba on the head)
Simba: Ow! Jeez, what was that for!?
Rafiki: It doesn’t matter. It’s in the past.
Simba: Yeah, but it still hurts.
Rafiki: Oh yes, the past can hurt. But the way I see it, you can either run from it... or learn from it.
It is here, in this moment of recursive insight—where the pain of the past becomes fuel for transformation—that the old trajectory fractures and a new one takes shape.
The diagram below brings together everything we’ve explored so far—attractors, phase transitions, narrative, and transformation—by mapping Simba’s journey onto the deeper mythological structure that underlies it. This figure was made by superimposing images onto figure 38 from Jordan Peterson’s Maps of Meaning.
At the top of the image, we see Simba’s original attractor: the carefree hedonism of Hakuna Matata. This state is stable, but suboptimal—resilient enough to endure, but too safe to foster growth. Then, the system is perturbed. Nala appears, an embodiment of the anomaly: both threat and promise, judgment and invitation. This encounter pushes Simba out of his equilibrium and into chaos, initiating the descent. Through confrontation, guidance, and reflection, Simba undergoes a nonlinear reconfiguration. As is often true of deep personal change, the transformation takes on the weight of a religious experience.
His return to the Pride Lands—transformed and resolute—marks not a return to his former self, but the emergence of a new attractor: deeper, more integrated, more complex. In this way, The Lion King enacts what myth has always encoded, and what complexity science now confirms: lasting transformation is born not from resistance to disruption, but through it.
A compelling case can now be made: the meta-mythology we have traced—the Hero’s Journey as revealed through Simba’s transformation—is not merely a narrative arc. It is a strange attractor in the technical sense: a patterned structure of change that arises spontaneously within complex dynamical systems. Let us walk through the reasons why:
1. The meta-mythology is structured, but non-repeating.
A strange attractor confines a system within a particular range of motion, but never along the same path twice. So too with myth. The structure—departure, descent, transformation, return—is recognizable across cultures and stories, yet its manifestations are endlessly varied. Simba’s arc shares a topological form with that of Odysseus, Moses, and Horus. But it is not a mechanical template. The story’s shape remains, while its particulars are sculpted by history, context, culture, and character. In dynamical terms: each journey is a unique trajectory through a shared attractor basin—guided by form, but never determined by it.
2. The meta-mythology emerges at the border between order and chaos.
Strange attractors live at the critical boundary between rigidity and randomness. This is the only space where genuine transformation is possible. The Hero’s Journey unfolds along that border. The hero must depart from the known, the predictable, the safe—but not dissolve entirely into formlessness. The risk is real: too much chaos, and the system disintegrates. Too much order, and it cannot evolve. The optimal zone is metastability: poised, sensitive, dynamic. Simba’s carefree life under “Hakuna Matata” is too ordered to grow; Scar’s reign is chaos disguised as order. The true transformation—Simba’s return as a just king—emerges only through this traversal of the borderlands.
3. The meta-mythology is fractal across scale.
Strange attractors are scale-invariant: their structure repeats at every level of analysis. The same is true of this mythic structure. It describes not only individual development (as in Simba’s journey), but the evolution of societies, revolutions, renaissances, religious awakenings. The pattern echoes across scales—from a child’s moral awakening to a civilization’s transformation. Myth is not simply symbolic—it is recursive structure, a map of how open systems reorganize under pressure.
4. The meta-mythology is a constraint that enables.
As Alicia Juarrero argues, strange attractors do not control systems like a blueprint. They act as context-sensitive constraints that shape without dictating. Myth, understood in this way, is not a script but a grammar of becoming. It narrows the infinite into the intelligible. It allows stories to diverge while remaining legible. This is the paradox of real guidance: not prescription, but possibility. Just as a strange attractor governs the evolution of a dynamical system without enforcing a path, the Hero’s Journey governs transformation without foreclosing creativity.
In sum:
What we call the Hero’s Journey—what Campbell named monomyth, what Peterson mapped as metamyth, and what countless cultures have encoded in story—is not simply narrative. It is the strange attractor representing the optimal pattern of transformation for complex systems. It does not dictate destiny, but outlines the structure of meaningful change. It is not metaphorical, but formal—a basin of possibility into which systems fall when their old patterns are shaken. Myth and complexity science converge here, showing us that real change is recursive and unstable, but not directionless. There is a shape to becoming.
Conclusion: Toward a Physics of Freedom
The classical scientific worldview—Newtonian, mechanistic, timeless—could not make sense of becoming. It explained motion but not transformation, structure but not emergence. Within that paradigm, freedom was either an illusion or an exception—something smuggled in from outside the system. But complexity science has changed the game. In the study of nonlinear dynamical systems, becoming is no longer an anomaly. It is the rule. The strange attractor, the phase transition, the recursive feedback loop—these are not deviations from nature’s logic. They are nature’s logic, once life and mind are taken seriously as real phenomena.
What this chapter has tried to show is that we now possess a scientific vocabulary for what myth, philosophy, and experience have long intuited: living systems persist not through stasis but through transformation; not by resisting perturbation, but by harnessing it. Complexity science offers us, at last, a physics of change—and with it, a physics of freedom.
This is where Nietzsche enters. Against the backdrop of a deterministic cosmos, he proclaimed the primacy of becoming over being. He denied the metaphysical comfort of static and timeless truth, urging instead an ethics of dynamical strength: to affirm life as flux, to embrace the chaos from which new orders emerge. The Übermensch, in this light, is not a final state but a metastable trajectory—a form resilient enough to endure transformation, porous enough to be remade. It is no accident that Nietzsche found inspiration in myth, tragedy, and the eternal recurrence. He grasped—prophetically—that the self is a complex system, and that freedom lies not in resistance to chaos, but in riding the wave with grace and style.
Thus the lesson: one must become durable through change, not against it. Rigidity shatters. Fragility retreats. But the resilient system—the wise soul, the just institution, the evolving species—dances at the edge of chaos. It does not cling to what is, but participates in what becomes. It learns from disruption. It reorganizes without dissolving. It says yes.
Yes to the past that still hurts.
Yes to the future that cannot be known.
Yes to the journey that could transform us—or destroy us.
A sacred Yes.
In the next chapter, we will examine in more detail how and why complexity emerges at the border between order and chaos. For now, it is enough to have glimpsed the truth: the self, the culture, the cosmos—all are in motion. And to live well is to learn how to dance with them, always on the edge of chaos.
Heraclitus, Nietzsche, Alfred North Whitehead, Laotzi (author of the Tao Te Ching), and many more.
Have you read Whitehead? I talked to Matt Segall recently about Whitehead, God and reality's trajectory (the podcasr will come out soon). It feels relevant to this. A lot of the things I've been thinking about recently have been making me want to go back to your work. So I'm glad you posted this, it's great !
Another excellent article Brett. Really enjoyed reading this and learning from you. I'm also happy to see you posting again and I - together with some friends on a private forum - have already committed to buying your book when it emerges from chaos.
I look forward to future instalments. Wishing you creativity, diligence and perservance. KEEP IT UP!